[백준] 2585 경비행기

March 29, 2021 ( last updated : March 29, 2021 )
이분탐색 그래프탐색 bfs dfs 알고리즘 algorithm

https://github.com/sneakstarberry/

Abstract

[백준] 2585번 경비행기

[백준] 2585번 경비행기

백준 2585번

알고리즘 유형

문제 이해

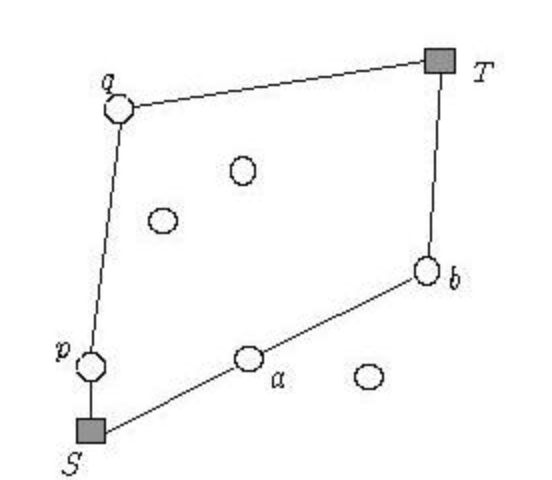출발점(S) = {0,0}, 도착점(T) = {10000, 10000} 까지 가는 도중에 k번 이하 경유할 때 최소의 거리를 구하면 된다. k번 이하가 중요하다.

풀이방법

보자마자 문제는 이분탐색과 bfs 혹은 dfs를 써야한다는 것을 알았다. 비슷한 문제 유형을 많이 풀다보니 그냥 알게 된 것 같다. 하지만 이런 혼합형은 처음이었다.

여기서 알고 있던 것은 bfs로 탐색한 결과가 이분탐색에서 mid 값이 low가 될 것 인지 high가 될 것인지 결정하는 결과 겂이 될 것 이라는 것. 그리고 mid 값은 가장 적은 연료로 추정되는 값이라는 것 또한 알았다.

하지만 문제가 되는 것은 시작 점에서 도착점까지 거리를 측정하면서 갈 때 어떻게 k번을 맞추면서 가냐는 것이었다. 근데 k번 이하라서 상관없는 고민이었다. 오히려 k번 이하라는 조건이 다른 경우의 수를 거르는 거름망이 되었다.

풀이는 간단하다. 점을 bfs방식으로 방문하면서 매번 도착점까지 걸리는 연료의 값을 구해서 최소 연료 소모 추정값(mid)과 비교해서 가능한지 확인한다. 가능하면 high가 mid가 되고 불가능하면 low가 mid가 된다. k번 이하인지는 큐에 방문 노드 개수를 넣어두면된다. 해당 발상은 다른 bfs문제에서 해봐서 쉬웠다.

#include <cstring>
#include <iostream>
#include <math.h>
#include <queue>

using namespace std;

int n, k, is_visited[1011];
double fuel(pair<int, int> _point1, pair<int, int> _point2);

int main() {
  ios::sync_with_stdio(false);
  cin.tie(NULL);

  pair<int, int> point[1011];
  cin >> n >> k;

  for (int i = 0; i < n; i++) {
    cin >> point[i].first >> point[i].second;
  }

  int l, h, m, minimum;
  l = 0;
  h = 20001;
  minimum = 20001;

  while (l + 1 < h) {
    memset(is_visited, 0, sizeof(is_visited));
    int reach = 0;

    m = (h + l) / 2;
    queue<pair<pair<int, int>, int>> q;
    q.push({{0, 0}, 0});

    while (!q.empty()) {
      int x = q.front().first.first;
      int y = q.front().first.second;
      int cnt = q.front().second;

      q.pop();
      if (cnt > k) {
        reach = 0;
        break;
      }
      if (fuel({10000, 10000}, {x, y}) <= m) {
        reach = 1;
        break;
      }

      for (int i = 0; i < n; i++) {
        if (is_visited[i])
          continue;
        int nx = point[i].first;
        int ny = point[i].second;

        if (fuel({nx, ny}, {x, y}) <= m) {
          q.push({{ nx, ny}, cnt + 1});
          is_visited[i] = 1;
        }
      }
    }

    if (reach) {
      minimum = m;
      h = m;
    } else {
      l = m;
    }
  }
  cout << minimum;
}

double fuel(pair<int, int> _point1, pair<int, int> _point2) {
  int _x = _point1.first - _point2.first;
  int _y = _point1.second - _point2.second;
  int _x_distance = _x * _x;
  int _y_distance = _y * _y;

  double _fuel = sqrt(_x_distance + _y_distance) / 10;

  return _fuel;
}

Originally published March 29, 2021
Latest update March 29, 2021

Related posts :

{# #}